
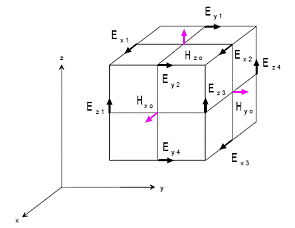
Meep simulates Maxwell's equations, which describe the interactions of electric () and magnetic () fields with one another and with matter and sources. For tutorial examples which demonstrate core functionality, see Tutorial/Basics and this projects page. Instead, the focus here is on the physics and numerical methods. This introduction does not describe the Python Interface with which you set up simulations. Also, FDTD is only one of several useful methods in computational electromagnetics, each of which has their own special uses - a few of the other methods are mentioned, and some hints are provided as to which applications FDTD is well suited for and when you should potentially consider a different method. This section introduces the equations and the electromagnetic units employed by Meep, the FDTD method, and Meep's approach to FDTD. This is a widely used technique in which space is divided into a discrete grid and the fields are evolved in time using discrete time steps - as the grid and the time steps are made finer and finer, this becomes a closer and closer approximation for the true continuous equations, and one can simulate many practical problems essentially exactly. Meep implements the finite-difference time-domain ( FDTD) method for computational electromagnetics.




 0 kommentar(er)
0 kommentar(er)
